Dilatações

Dilatação superficial

 Os corpos, quando submetidos à variação de temperatura, têm as suas dimensões alteradas, essa variação é chamada de dilatação térmica.

A dilatação superficial é aquela na qual ocorre variação na área do corpo. Considere a placa metálica descrita na gravura abaixo:

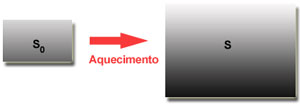
  Inicialmente, a temperatura inicial é to, a placa tem área inicial So. Após ser aquecida por uma fonte de calor, a sua área ganha novas dimensões, ou seja, ela se expande em razão do aumento no grau de agitação das moléculas que a compõem. Agora com temperatura final t, a placa metálica passa a ter área final S. A variação de área sofrida pela placa pode ser determinada da seguinte forma:

ΔS = S – So

Dilatação linear

A dilatação linear é aquela em que ocorre variação em apenas uma dimensão, ou seja, o comprimento do material. Imagine a seguinte situação: uma barra de metal de comprimento Li à temperatura ti, é aquecida até uma determinada temperatura tf. O que se percebe é que a barra, após o aquecimento, não tem mais o mesmo comprimento, ou seja, ela sofreu uma variação na sua dimensão, no seu comprimento, ela se dilatou. Veja:

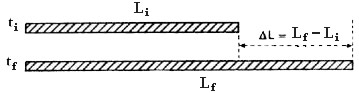
 Onde ΔL = Lf – Li é a variação do comprimento, ou seja, a dilatação linear da barra. E Δt = tf – ti é a variação da temperatura da barra. Experimentalmente verifica-se que:

- o comprimento inicial (Li) é proporcional à temperatura inicial (ti);

- o comprimento final (Lf) é proporcional à temperatura final (tf);

- a dilatação linear depende do material que constitui a barra.

Mediante essas constatações foi determinada a seguinte equação para dilatação linear dos corpos: ΔL = Liα Δt, onde α é denominada de coeficiente de dilatação linear, é uma constante característica do material que constitui o corpo. Por exemplo, para o alumínio temos que α = 0,000023 por °C (ou °C-1), isso quer dizer que o alumínio dilata 23 milionésimos de seu comprimento a cada 1°C de variação na sua temperatura, ou seja, uma dilatação muito pequena e que possivelmente só pode ser vista em microscópio.

Dilatação volumétrica

 Nesse tipo de dilatação podemos dizer que o corpo sofre variação de tamanho em todas as dimensões (comprimento, largura e altura), como mostra a figura:

 Vamos considerar um corpo de volume V0 à temperatura T0 e volume V à temperatura T. A variação de volume (ΔV) e a variação de temperatura (ΔT) são definidas da seguinte maneira:

ΔV = V – V0  e  ΔT = T – T0

Dilatação aparente

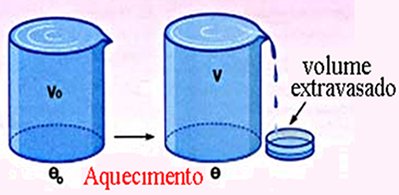
Sabemos que os líquidos dilatam-se obedecendo às mesmas leis que estudamos para os sólidos. No entanto, como os líquidos não têm forma própria, mas tomam a forma do recipiente, somente tem significado o estudo de sua dilatação volumétrica.

Quando se observa a dilatação de um líquido, ele está obrigatoriamente contido em um frasco que é aquecido simultaneamente com ele. Assim, ambos se dilatarão e, como a capacidade do frasco aumenta, a dilatação que observaremos, para o líquido, será uma dilatação aparente. A dilatação real do líquido será maior do que a dilatação aparente, observada.

Essa dilatação real é, evidentemente, igual à soma da dilatação aparente com a dilatação volumétrica do recipiente. Quando usamos um recipiente cujo coeficiente de dilatação é muito pequeno, a dilatação aparente do líquido torna-se praticamente igual à sua dilatação real.

Suponhamos que, em um experimento, o líquido em estudo preencha completamente o recipiente, na situação inicial. Para efeitos práticos, consideraremos que o volume inicial do líquido pode extravasar, em decorrência da dilatação.

A dilatação aparente do líquido também é proporcional ao volume inicial, Vo e à variação de temperatura, Δθ, de modo que:

Nessa expressão, Yaparente é o coeficiente de dilatação do líquido. Sabemos também que a variação do volume do frasco é:

Naturalmente, o aumento real do volume do líquido deve corresponder ao volume do líquido extravasado somado ao aumento do volume do frasco. Em outras palavras, o aumento real do volume do líquido corresponde à quantidade do líquido que se derrama, mais a quantidade de líquido que transbordaria se o recipiente (frasco) não sofresse nenhuma dilatação. Dessa forma, temos: 

A partir dessa equação, podemos obter:

Essa expressão permite concluir que a dilatação aparente de um líquido depende da natureza do líquido e do recipiente em que ele é colocado para ser aquecido. 

Fontes:

http://www.brasilescola.com/fisica/dilatacao-superficial.htm

http://www.brasilescola.com/fisica/dilatacao-linear.htm

http://www.brasilescola.com/fisica/dilatacao-volumetrica.htm

http://www.brasilescola.com/fisica/dilatacao-aparente.htm